V神新作：一文了解什么是\tPLONK

摘要：零知识证明新突破。

今年8月底，AZTEC协议官推宣布，开发出了PLONK，这是一种全新的高效通用ZK-SNARK架构。PLONK只需要一个可信设置，所有程序都可以重复使用这个设置。PLONK足以在以太坊上被实际采用。

以太坊 2.0 研究员 Justin Drake 称，PLONK 是一种全新的零知识证明系统，支持通用或可更新的可信设置（trusted setup），而且相比 Sonic 有显著的性能提升。这将会是在真实环境中使用零知识证明的一个巨大进步，并且不会由于可信设置而产生信任问题。

鉴于零知识证明技术衍生出了太多的术语名词，在使用中很容易被混淆。近日，以太坊创始人V神在其博客上发布了一篇名为“understand PLONK”的文章，以便人们更容易了解到底什么是PLONK。

以下为该博客全文：

最近，Ariel Gabizon（Filecoin 母公司 Protocol Labs 的研究员）、Zac Williamson和Oana Ciobotaru（Aztec Protocol 的两名研究人员 ）宣布了一种新的通用的零知识证明方案PLONK。

虽然通用零知识证明协议已经改进多年，但PLONK(以及更早但更复杂的Sonic和最近的Marlin)带来的是一系列的增强，可以极大地提高这些类型证明的可用性和进展。

第一个改进是，虽然PLONK仍然与Zcash中的snark有着类似的可信设置过程，但它是一个“通用的、可更新的”可信设置。

这意味着两件事：

1、你想证明的不是每个程序都有一个独立的可信设置，整个方案只有一个可信的设置，在此之后，您可以将该方案用于任何程序(在进行设置时选择的最大尺寸)。

2、有一种方法可以让多方参与受信任的设置，只要其中一方是诚实的，那么该设置就是安全的，而且这种多方参与的过程是完全按顺序的:第一个人参与，然后是第二个，然后是第三个……所有参与者甚至不需要提前知道;新参与者可以把自己加到最后。这使得可信设置很容易拥有大量参与者，从而在实践中非常安全。

第二个改进是它所依赖的“fancy cryptography”是一个单一的标准化组件，被称为“polynomial commitment（多项式承诺）”。

PLONK使用“Kate commitment”，基于可信设置和椭圆曲线配对，但你可以用其他方案替换它，比如FRI(这将使PLONK变成一种STARK)或DARK(基于隐藏顺序组)。这意味着该方案在理论上兼容证明大小和安全性假设之间的任何(可实现的)折中。

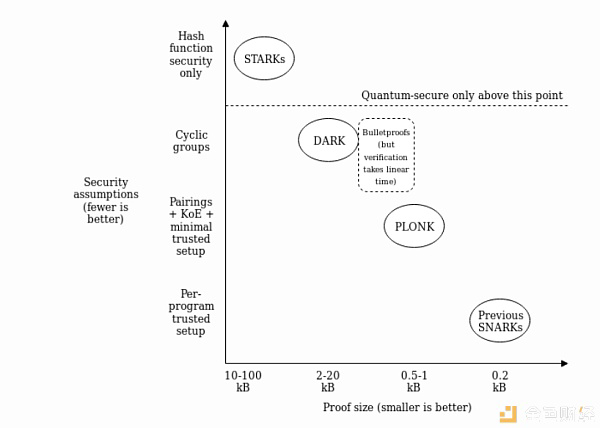
这意味着需要在证明大小和安全假设之间进行不同权衡的用例(或者对于这个问题有不同意识形态立场的开发人员)仍然可以共享大部分相同的“算术化”工具——将一个程序转换成一组多项式方程的过程，然后用多项式承诺来检查这些方程。如果这种方案被广泛采用，我们可以期待在改进共享算术化技术方面取得快速进展。

PLONK是怎样工作的

让我们从解释PLONK是如何工作开始，以某种抽象的格式，侧重于多项式方程，而不是立即解释如何验证这些方程。

PLONK的一个关键组成部分，就像snark中使用的QAPs一样，是一个转换问题形式的过程，从“给一个值X，使用特定程序P，当用X作为输入求值时，得到特定的结果Y。”变成了"给我一组值满足一组数学方程"。

（注：QAP - Quadratic Arithmetic Program，QAP 问题，是实现基于算术电路的 NP 问题的证明和验证）

程序P可以表示很多东西，例如，问题可以是“给我一个sudoku的解”，你可以通过设置P为一个sudoku验证器加上一些初始值编码，并设置Y为1(即："是的，这个解是正确的")，

一个令人满意的输入X将是sudoku的有效解。这是通过把P表示成一个带逻辑门的电路，用于加法和乘法，并把它转换成一个方程组，其中变量是所有导线上的值，每个门有一个方程(例如：x6 = x4 * x7，加法 x8 = x5 x9)。

（注：算术电路可以简单看成由三种门组成：加门，系数乘法门以及通用乘法门（减法可以转化为加法，除法可以转化为乘法）。Vitalik 在 2016 年写过的 QAP 介绍（https://medium.com/@VitalikButerin/quadratic-arithmetic-programs-from-zero-to-hero-f6d558cea649），深入浅出的解释 NP 问题的算术电路生成和 QAP 问题的转化）

下面是一个求x的例子，P(x) = x**3 x 5 = 35(提示:x = 3):

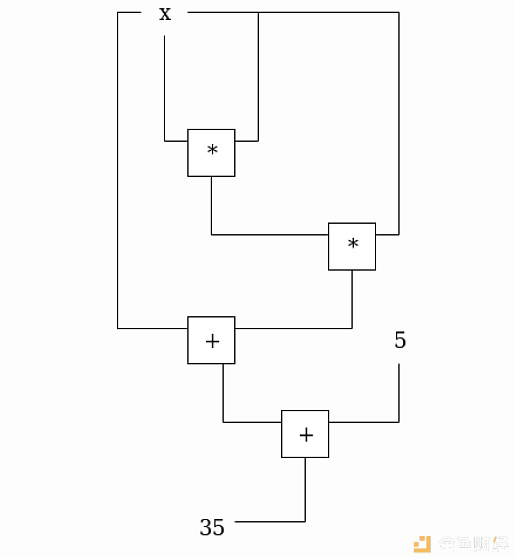
我们可以给这些门和电路贴上如下标签:

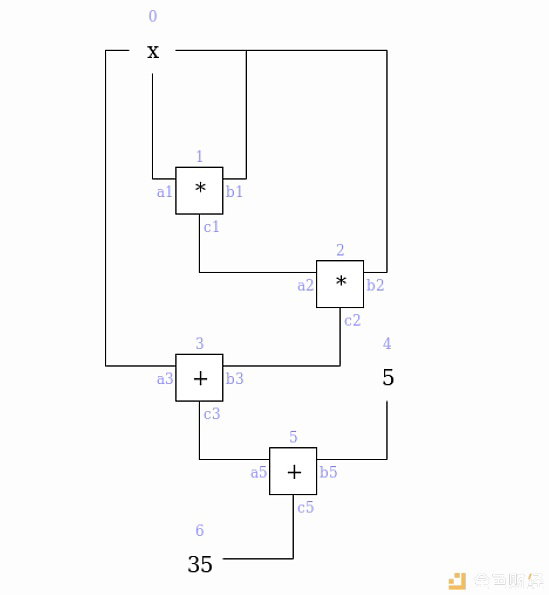
在门和电路上，我们有两种约束:门约束(同一门上的电路之间的方程式，例如：a1 * b1 = c1)和复制约束(关于电路中任意位置不同电线的相等性的声明，例如：a0 = a1 = b1 = b2 = a3或c0 = a1)。我们将需要创建一个结构化的方程组，它最终将减少到一个非常少的多项式方程，以表示两者。

（注：QAP 问题是这样一个 NP 问题：给定一系列的多项式，以及给定一个目标多项式，找出多项式的组合能整除目标多项式。）

在PLONK中，这些方程的设置如下。每个方程的形式如下(想想:L =左，R =右，O =输出，M =乘法，C =常数):

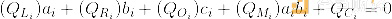
每个Q值都是一个常数，每个方程中的常数(以及方程的数量)对于每个程序都是不同的。每个小写的值都是一个变量，由用户提供:ai是第i个门的左输入线，bi是右输入线，ci是第i个门的输出线。对于加法门，我们设置:

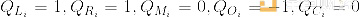
把这些常数代入方程，化简得到ai bi - oi = 0，这正是我们想要的约束条件。对于乘法门，我们设:

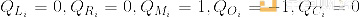
对于将ai设为某常数x的常数门，我们设:

您可能已经注意到，一根电路的每一端以及一组电路中的每一根电路都必须具有相同的值(例如，对应一个不同的变量。到目前为止，还没有强迫一个门的输出与另一个门的输入相同的东西(我们称之为“复制约束”)。

PLONK当然有一种强制执行副本约束的方法，但是我们将在稍后进行讨论。现在我们有一个问题，验证者想要证明他们有一堆xai 、xbi、 xci值满足一堆相同形式的方程。这仍然是一个大问题，但与“为这个计算机程序找到一个满意的输入”不同，这是一个非常结构化的大问题，我们有数学工具来“压缩”它。

从线性系统到多项式

如果您已经阅读过关于STARKs或QAPs的内容，那么在下一节中描述的机制可能会让您感到有些熟悉，但是如果没有，也没有关系。这里的主要内容是将多项式理解为一个数学工具，用于将大量的值封装到一个对象中。通常，我们认为多项式的“系数形式”，这是一个表达式，如:

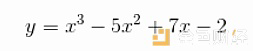
但我们也可以在“求值表”中查看多项式。例如，我们可以把上面的看成是在坐标(0,1,2,3)处分别求值(- 2,1,0,1)的< 4次多项式。

这是下一步。许多相同形式的方程组可以重新解释为多项式上的一个方程。例如，假设我们有这样一个系统:

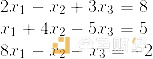
让我们定义四个多项式的求值形式:

L(x)是在坐标(0,1,2)处取值为(2,1,8)的次数< 3多项式。在相同的坐标下，M(x)的值为(- 1，4，1)，R(w)为(3，-5，-1)和O(x)为(8，5，-2)(这样直接定义多项式是可以的，可以使用拉格朗日定理（Lagrange interpolation）将其转换为系数形式)。现在，考虑这个等式:

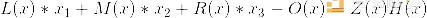
这里，Z (x)是(x) * (x - 1) * (x - 2)的缩写——-在计算域(0,1,2)上返回0的最小(非平凡)多项式。这个方程(x1 = 1, x2 = 6, x3 = 4 H(x) = 0)的解也是原方程组的解，只是原方程组不需要H(x)。

还要注意，在这种情况下，H(x)很方便地为零，但在更复杂的情况下，H可能需要非零。

现在我们知道，我们可以用一小部分数学对象(多项式)来表示大量的约束条件。但是在我们上面用来表示门约束的方程中，每个方程的x1, x2, x3变量是不同的。我们可以通过使变量本身多项式而不是常数来处理这个问题。所以我们得到:

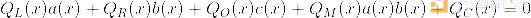
和以前一样，每个Q多项式都是一个参数，可以从正在验证的程序中生成，而a、b、c多项式是用户提供的输入。

复制约束

现在，让我们回到“连接”电路。到目前为止，我们所拥有的只是一堆关于不相交值的不相交方程，它们很容易独立满足:常数门可以通过将值设置为常数来满足，加法和乘法门可以通过将所有线设置为零来满足！为了使问题真正具有挑战性(并实际表示在原始电路中编码的问题)，我们需要添加一个验证“复制约束”的方程:约束如a(5) = c(7)， c(10) = c(12)，等等。这需要一些巧妙的技巧。

我们的策略是设计一个“坐标对累加器”，一个多项式p(x)，其工作原理如下：

首先，设X(X)和Y(X)是两个多项式，表示一组点的X和Y坐标(例如：要表示集合((0,2)，(1,1)，(2,0)，(3,1))，可以令X(X) = X, Y(X) = x3 - 5x2 7x -2))。我们的目标是让p(x)表示到(但不包括)给定位置的所有点，因此p(0)从1开始，p(1)表示第一个点，p(2)表示第一个和第二个点，我们将通过“随机”选择两个常数，v1和v2，利用约束条件p(0) = 1和p(x 1) = p(x) * (v1 x (x) v2 * Y(x))构造p(x)，至少在定义域(0,1,2,3)内。例如，令v1 = 3, v2 = 2，得到:

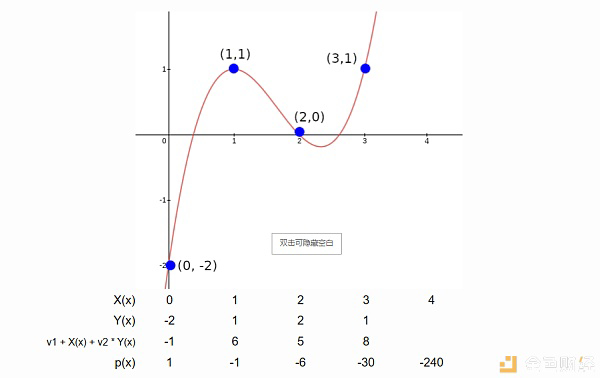
注意(除了第一列)每个p(x)值都等于它左边的值乘以它左边和上面的值。

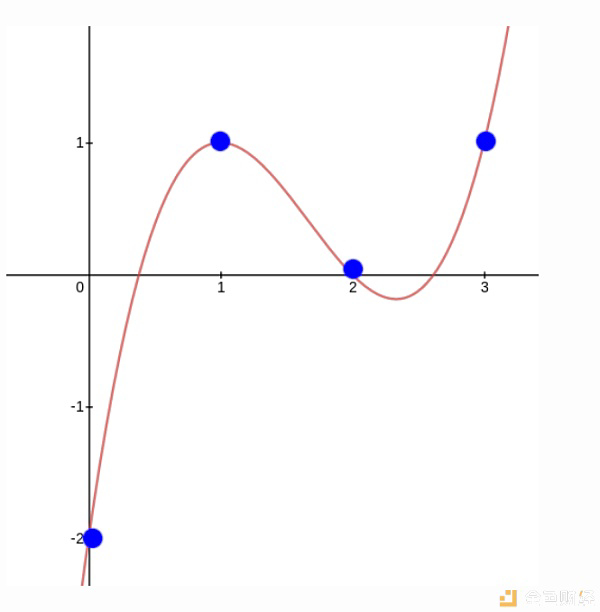
我们关心的结果是p(4) = -240。现在，考虑这样一种情况，不是X(X) = X，而是X(x) = ²⁄₃ x³ - 4x^{2 19}⁄₃ x(即在坐标(0,1,2,3)处取值为(0,3,2,1)的多项式)。如果运行相同的过程，还是会得到p(4) = -240。

这不是巧合(事实上，如果你从一个足够大的场中随机选取v1和v2，它几乎不会碰巧发生)。相反,这是由于Y(1)= Y(3),所以如果你“交换X坐标”的点(1,- 1)和(3,1)，你不会改变这些点的集合,因为累加器编码一个集合(因为乘法不关心顺序)，所以最后的值是相同的。

现在我们可以开始学习证明复制约束的基本技术。首先，考虑一个简单的例子，我们只想证明一组连接中的复制约束(例如：我们要证明a(1) = a(3)。

我们将创建两个坐标累加器:一个是X(X) = X和Y(X) = a(X)，另一个是Y(X) = a(X)。但X ' (X)是一个多项式，它的计算结果是每个复制约束中翻转(或重新排列)值的排列。在a(1) = a(3)的情况下，这意味着置换将从0 3 2 1 4开始…第一个累加器是压缩（（0，a（0）），（1，a（1）），（2，a（2）），（3，a（3）），（4，a（4））…第二个（（0，A（0）），（3，A（1）），（2，A（2）），（1，A（3）），（4，A（4））……只有当a（1）=a（3）时，两者才能给出相同的结果。

为了证明a、b和c之间的约束条件，我们使用相同的过程，将三个多项式的点“累加”在一起。我们给a、b、c各指定一个X坐标范围(例如。a得到 Xa(x) = x ie. 0...n-1, b得到Xb(x) = n x, ie. n...2n-1，c得到Xc(x) = 2n x, ie. 2n...3n-1。为了证明在不同的连接集之间跳转的复制约束，“备用”X坐标将是跨所有三个集合排列的切片。例如，如果我们想用n = 5证明a(2) = b(4)，那么X’a(x) 的值为0 1 9 3 4,以及X’b(x)的值为5 6 7 8 2(注意2和9翻转了，其中9对应于b4 导线)。

然后，我们将不再在一个过程的运行中检查等式(即检查p(4) = p '(4)。如前所述，我们将检查每边三种不同运行的乘积:

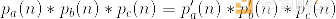
每边的三个p(n)值的乘积累加了a、b和c中所有的坐标对，因此，这允许我们像以前一样进行相同的检查，除了我们现在可以检查复制约束，不仅在三组导线a、b或c中的一组内的位置之间，而且在一组导线和另一组导线之间。就像在a(2) = b(4)中一样。

就是这样!

把它们放在一起

实际上，所有这些数学运算不是针对整数，而是针对一个素数字段。也不是用x=0...n-1表示电路的指数。

我们将使用ω的能力:1、ω, ω2….ωn-1 。其中ω是一个高阶root-of-unity。这不会改变数学，除了坐标对累加器约束检查方程发生了变化。从p(x 1) = p(x) * (v1 X(x) v2 * Y(x)) to p(ω * x) = p(x) * (v1 X(x) v2 * Y(x)),而不是使用0..n-1, n..2n-1, 2n..3n-1作为坐标，我们使用ωi g *ωi和g2 *ωi g可以是一些随机的高阶元素。。

现在我们把需要检查的方程都写出来。首先，主要的门约束满意度检查:

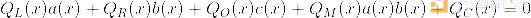
然后多项式累加器转换约束(注意:把“= Z(x) * H(x)”理解为“在我们关心的某个特定域中的所有坐标都等于零，但不一定在它之外”):

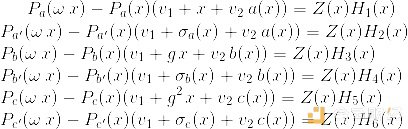
然后多项式累加器的启动和结束约束:

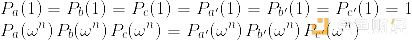
用户提供的多项式为：

电路分配：a(x)， b(x)， c(x)

累积坐标：Pa(x)， Pb(x)， Pc(x)， Pa(x)， Pb(x)， Pc(x)

The quotients：H(x)和H1(x).. H6(x)

验证者需要提前计算的程序特定多项式为:

QL(x)、QR(x)、QO(x)、QM(x)、QC(x)，它们一起表示电路中的门(注意QC(x)编码公共输入，因此可能需要在运行时计算或修改)

“置换多项式”在a、b和c电线之间，σa(x), σb(x) and σc(x)的编码复制约束。

注意，验证器只需要存储对这些多项式的承诺。唯一剩下的多项式在上面的方程Z(x) = (x - 1) * (x - ω) * … * (x - ω^n-1)旨在评估所有这些点为零。幸运的是,ω可以选择把这个多项式很容易评估:通常的方法是选择满足ωⁿ = 1,在这种情况下,Z(x) = xⁿ - 1。

v1和v2的唯一约束是，当v1和v2已知后，用户不能选择a(x)、b(x)或c(x)，所以我们可以通过计算从a(x)、b(x)和c(x)的承诺哈希值计算v1和v2来满足这一点。

现在我们已经把程序满足问题变成了一个简单的用多项式来满足几个方程的问题，PLONK中有一些优化可以让我们去掉上面方程中的许多多项式，为了保持简单，我就不讲了。但是多项式本身，包括特定于程序的参数和用户输入，都很大。下一个问题是，我们要怎么做才能让证明更简短?

多项式承诺

多项式承诺是一个简短的对象，它“表示”一个多项式，并允许你验证该多项式的计算结果，而不需要实际包含该多项式中的所有数据。

也就是说，如果有人给你一个代表P(x)的承诺c，他们可以给你一个证明来说服你，对于某个特定的z, P(z)的值是多少。

还有一个进一步的数学结果表明，在一个足够大的域中，如果关于多项式的某些类型的方程(在z已知之前选择的)在随机z上取值为真，那么同样的方程对于整个多项式也成立。例如，如果P(z) * Q(z) R(z) = S(z) 5，那么我们知道，一般情况下P(x) * Q(x) R(x) = S(x) 5是极有可能的。使用这样的多项式承诺，我们可以很容易地检查上面所有的多项式方程——做出承诺，用它们作为输入来生成z，证明每个多项式在z处的计算值，然后用这些计算值来运行方程，而不是原始多项式。但是这些承诺是如何起作用的呢?

它包括两个部分:对多项式P(x) -> c的承诺，以及在某个z处对一个值P(z)的开放。一个例子是FRI，另一个例子是Kate commitment，我将在下面描述。为了证明一个开头，有一个简单的通用“减法除法”技巧:要证明P(z) = a，需要证明

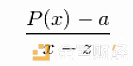
这也是一个多项式(使用另一个多项式承诺)。这是因为如果quotients是一个多项式，那么x - z是P(x) - a的一个因子，所以(P(x) - a)(z) = 0，所以P(z) = a。

用多项式试试，例如：P(x) = x³ 2*x² 5 加上(z = 6, a = 293)试试(z = 6, a = 292)看看它是如何失败的。

还请注意一个泛型优化:为了同时证明多个多项式的多个开口，在提交到输出之后，对多项式和输出的随机线性组合执行减法和除法技巧。

那么承诺本身是如何起作用的呢?幸运的是，Kate承诺比FRI简单得多。一个可信的设置程序生成一组椭圆曲线点G, G * s, G * s² …. G * sⁿ。和G2 * s一样，其中G和G2是两个椭圆曲线群的生成器，而s是一个秘密，一旦这个过程完成，就会被忘记。(注意，这个设置有一个多方版本，只要至少有一个参与者忘记了他们的秘密，这个设置就是安全的)。

这些要点被公布，并被认为是本计划的“证明重点”。任何需要做出多项式承诺的人都需要用到这些点。对d次多项式的承诺是将证明键的前d 1个点乘以多项式中相应的系数，并将结果相加。

注意，这提供了一个多项式在s处的“求值”，而不需要知道s。例如, x³ 2x² 5 可以用(G * s³) 2 * (G * s²) 5 * G表示。我们可以使用符号[P]来表示以这种方式编码的P(即。G * P (s))。做加减乘除运算的技巧时,你实际上可以证明两个多项式满足的关系,利用椭圆曲线组合:检查e ([P] - G *, G2) = e([Q],[x] - G2 * z)作为检查代理P(x) - a = Q(x) * (x - z)。

但是最近也出现了其他类型的多项式承诺。一种称为DARK的新方案(“Diophantine knowledge arguments”)使用“隐藏的有序组”来实现另一种多项式承诺。隐藏顺序组是唯一的，因为它们允许您将任意大的数字压缩为组元素，甚至比组元素大得多的偶数，以一种不能“欺骗”的方式;从VDFs到累加器，从范围证明到多项式承诺，都可以建立在此基础上。

另一种选择是使用防弹证明，使用规则椭圆曲线组，代价是证明花费的时间要长得多。由于多项式承诺比完全的零知识证明方案要简单得多，我们可以期待在未来会产生更多这样的方案。

回顾

最后，让我们再看一遍这个计划。给定一个程序P，你把它转换成一个电路，然后生成一组这样的方程:

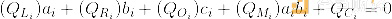
然后将这组方程转换成一个多项式方程:

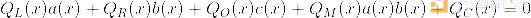
您还可以从电路中生成一个复制约束列表。从这些副本约束生成三个代表交换电路指数多项式:σa (x)，σb (x)，σc (x)。要生成一个证明，需要计算所有这些电路的值并将它们转换成三个多项式:a(x)，b(x)，c(x)。您还可以计算6个“坐标对累加器”多项式，作为置换检查参数的一部分。最后计算Hi(x)。

多项式之间有一组方程需要检查，你可以通过对多项式做出承诺，在任意z点打开它们(并证明这些开口是正确的)，然后在这些计算上运行方程，而不是在原始多项式上运行。证明本身只是一些承诺和开始，可以用几个方程来检验。就是这样!

原文链接：

https://vitalik.ca/general/2019/09/22/plonk.html

作者：Vitalik Buterin

编译：共享财经Neo