比特币期货合约大额挂单价格位置的统计推断——核密度估计法

派客国际投资（集团）有限公司    苏文杰

摘要：本文对BitMEX交易所的XBTUSD永续合约的卖4000至买4000的市场深度数据进行统计分析，通过核密度估计得出了大额挂单在不同价格位置出现的概率密度。

大额挂单分为买单和卖单，前者可视为支撑位，后者可视为阻力位，它们对行情走向具有一定的影响。大额挂单的价格可能在限价指令薄的固定位置，也可能在一定的价格范围内移动，可假设其在较大概率上会出现在某些特定的价格位置，从而反映出各个挂单者对行情的判断。

本文对BitMEX交易所的XBTUSD永续合约的卖4000至买4000的市场深度数据进行统计分析，通过核密度估计得出了大额挂单在不同价格位置出现的概率密度。

从获取市场深度数据的时效性来讲，由于获取具有一定的延迟，所有的数据其实都是过去的数据，不一定能代表当前的大额挂单的价格位置，但根据它们在不同价格位置出现的概率密度，我们可以对下一时刻它们可能出现的价格位置做出推断，从而进行相应的策略决策。

不同的编程语言一般都有特定的不同的函数来专门运行核密度估计的计算，比较方便，但在实际情况中，为了使程序能够准确反映我们的意图，有必要去深入理解核密度估计的概念。

一、核密度估计[1]-[5]

（一）概率密度函数估计的简要介绍

概率密度函数，常简称为密度函数以至密度，是概率论的最重要概念之一。虽然在统计学上我们常提“总体分布”这个名词，但使用密度的概念去规定或刻画一个统计模型不仅常见，而且比使用分布概念更合适和方便。在各种实际问题中，变量取值的分布呈现“两头小、中间大，左右对称”这种“正态类似型”者为数颇多。这些特点在密度函数的图像上一目了然，而在分布函数的图像上则有不同。

密度估计问题，就是要通过从总体中抽得的样本去估计其概率密度函数f。在实际操作中，总可以把问题说成：固定一已知的x轴，要估计f在x点之值f(x)。

如果概率密度函数形状被假定或已知，那么就用参数估计法。如果概率密度函数的形状未知，则用非参数估计法。实际上一般不要求密度函数有某种特定的数学形式，如密度为正态分布之类，也就是说未知密度函数的所属类型并不知道。理由很明显：若密度函数的数学形式已知，而只含少量未知参数，则不如径直考虑这些参数的估计问题，而不提密度估计问题。因此，密度估计问题在本质上说是非参数性的。如今最流行的非参数密度估计法是核密度估计法，也称为Parzen密度估计法。

核密度估计作为一种非参数统计方法，在近四十余年吸引了不少学术界的注意，通过研究发现核密度估计的方法并非建立在某种艰深的概念或数学工具的基础上，而不过是古老的直方图方法的自然发展，这在统计发展史上有一定的代表性。应当指出的是，密度估计的重要性并不在于它的单独使用，而是作为统计推断的中间环节发挥作用。著名统计学专家Silverman曾指出，概率密度函数估计在数据统计处理的所有阶段都是有用的。

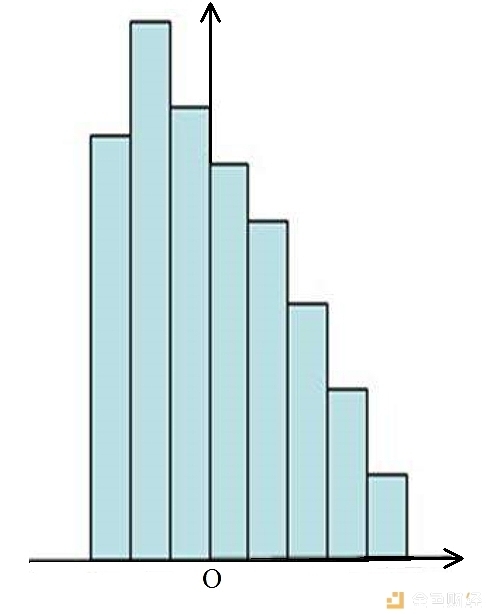
图1

在关于直方图的理论讨论中，我们常假定区间分隔（即上文a、h的选择）是在考察样本之前就定下来的，因此无随机性，这就使理论简化了。但在实际操作时不一定能恪守这个规定。例如，一批样本可能较集中在O点附近，而在较远的地方的个数较少。这时，有条件把密度f在O点附近之值估计得细一些，而在远处则只能满足于较粗的估计。也就是说，我们可能取一些不等长的区间，区间长度在O附近很短而在远离O点处则较长。然后在每一区间内按（1）式作出f的估计。这时，区间的位置、长短都是在参考了样本以后决定的，故有随机性。这样的直方图估计称为“Data-based”的直方图估计，其理论较a和h都比通常的直方图估计复杂得多，这里就不再讨论了。

直方图估计的优点在于简单易行，且在n较大而容许h较小的情况下，所得图像尚能显示密度的基本特征，但也有明显的缺点——它不是连续函数（这可以通过适当地修匀来解决），且从统计角度看效率较低。例如，在这一方法下，每一区间中心部分密度估计较准，而边缘部分则较差。综合种种因素，我们仍可以说：直方图估计不失为一个有用而基本的密度估计方法。

3、Parzen的核估计

不难看出：Rosenblatt估计仍为一个阶梯函数，只不过与直方图估计比起来，各阶梯之长不一定相同而已，仍非连续曲线。另外，从Rosenblatt估计的定义中看出，为估计f在x点之值f(x)，对与x在一定距离（确切地说，是h/2）内的样本，起的作用一样，而在此以外则毫不起作用。直观上可以设想：为估计f(x)，与x靠近的样本，所起的作用似应比远离x的样本要大些。这些在Parzen于1962年提出的核估计方法中都得到了体现。

为介绍Parzen的思想，我们先将（2）式变换一个形式，引进一个函数

（三）核函数的举例

以一维情况为例，常用的核函数见下表：

表1

根据上表所示，画出几类核函数的图像如下：

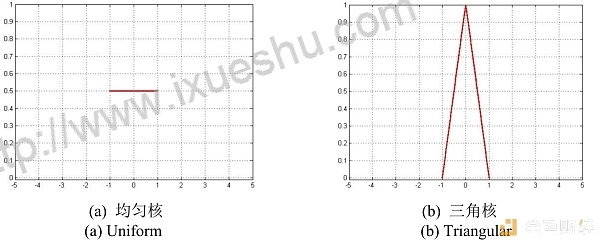
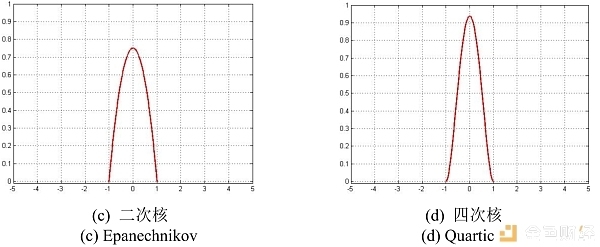
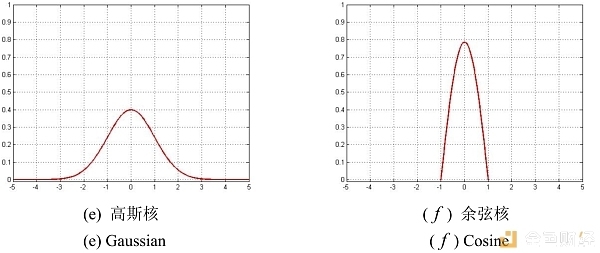
图2

二、比特币期货合约大额挂单的价格位置

不断获取BitMEX交易所的XBTUSD永续合约的卖4000至买4000的市场深度数据，将UTC时间2019-08-01 03:49:22时的数据绘图如下所示：

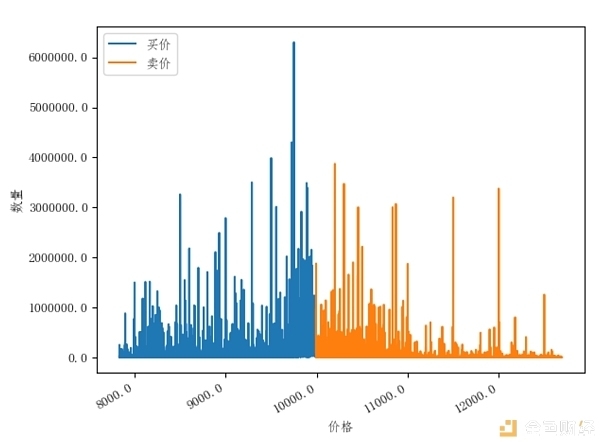
图3

将数据分为卖200至买200、卖800至买800、卖1600至买1600、卖3000至买3000、卖4000至买4000各段，分别求得各段的最大卖价和买价。只不断地保存最近一段时间（这里取3分钟）各段的最大卖价和买价，这可能就是潜在的支撑位和阻力位所在的价格位置。

根据保存的数据，利用核密度估计（采用高斯核函数）来计算出各段的支撑位和阻力位所在价格位置的概率密度，概率密度最大处附近即为支撑位或阻力位的所在位置。而各支撑位和阻力位所对应的限价单数量则分别来自于所保存的数据中对应的各限价单数量的中位数。

我们可以分别画出各段的概率密度图，为了方便观察，我们将各图绘制在一起，将阻力位用偏红色的线条表示，将支撑位用偏绿色的线条表示，可得下图：

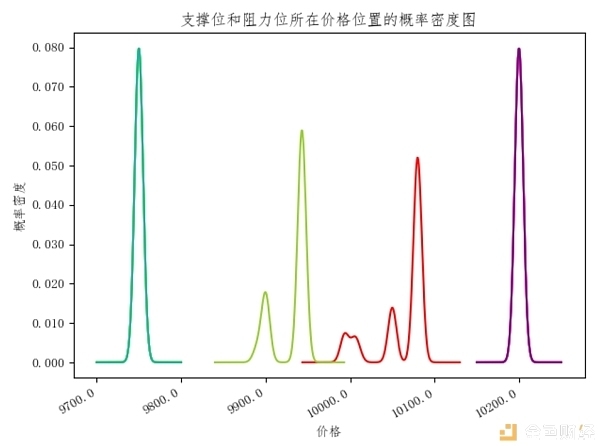
图4

上图各峰值附近即为大额挂单所形成的支撑位和阻力位，进一步将相关数据列表如下：

表2

从上表可知，各概率密度的峰值虽然不大，但在其邻域进行积分所得到的概率的值较大，因此各概率密度的峰值对应的价格位置附近就是各支撑位和阻力位的价格位置。

此外，各深度的支撑位和阻力位有部分重合。支撑位有两个：价格9750附近，数量（中位数）约为629.8万张；价格9943附近，数量（中位数）约为215.4万张；阻力位有两个：价格10080附近，数量（中位数）约为135.6万张；价格10200附近，数量（中位数）约为385.5万张。

我们可根据策略需求来选用这些支撑位和阻力位，例如，只将数量600万张以上的视为有效支撑位和阻力位，那么在这段行情就只在价格9750附近存在一个有效支撑位。又如，只将数量1000万张以上的视为有效支撑位和阻力位，那么在这段行情就暂时不存在有效支撑位和阻力位。

三、结论与讨论

本文对BitMEX交易所的XBTUSD永续合约的卖4000至买4000的市场深度数据进行统计分析，通过核密度估计得出了大额挂单在不同价格位置出现的概率密度，从而确定了各支撑位和阻力位的位置。在实际操作中，我们可以根据具体策略选用它们，只将限价单数量达到一定量的价格位置视为有效的支撑位和阻力位。

需要注意的是，比特币期货的波动性很大，支撑位或者阻力位或许只适用于震荡行情中的策略判断，当出现瀑布行情时，巨大的交易量使得它们比较容易被突破。因此，我们往往将其与其他指标一起使用来降低风险。

参考文献

[1] 陈希孺, 柴根象. 非参数统计教程. 上海: 华东师范大学出版社, 1993. 247-253

[2] 郭照庄. 密度核估计中最优窗宽选择的研究. 燕山大学硕士学位论文, 2006. 1-9

[3] 张玉敏. 基于不同核函数的概率密度函数估计比较研究. 河北大学硕士学位论文, 2010. 8

[4] 茹杨. 核函数的核密度估计算法. 哈尔滨理工大学硕士学位论文, 2016. 3-5

[5] 谢中华. MATLAB统计分析与应用：40个案例分析. 第二版. 北京：北京航空航天大学出版社, 2015. 209